RELACIONES METRICAS EN LOS TRIANGULOS OBTUSANGULOS

Nicolas Lobatschewski

Nacido en el año 1793. Es conocido por la ruptura con el pasado geométrico de Euclides.

Con su obra “PANGEOMETRÍA” este geómetra ruso rompió definitivamente con el pasado Euclidiano.

Fue criticado duramente, nadie le entendió ni le hizo caso, hasta que su memoria fue traducida al francés, en 1837 y al alemán en 1840.

Para Lobatschewski, las paralelas eran “RECTAS COPLANARÍAS QUE NO SE ENCUENTRAN POR MUCHO QUE SE LAS PROLONGUEN”.
Existe otra teoría suya que rompe con el postulado de Euclides

I.- TEOREMA DE EUCLIDES
1er Caso: si: a <>

a2 = b2 + c2 – 2bm

Ejemplo aplicativo

Hallar "x"

Resolucion:

Trazamos la altura como se muestra en la figura y conocemos los datos de los lados por triangulos rectangulos notables de 37º y 53º

Ahora aplicaremos el teorema de euclides:

x2 = 82+52 -2(8)(3); entonces calcuolaremos el valor de "x"

2do Caso: si: a > 90º

a2 = b2 + c2 + 2bm

Ejemplo aplicativo

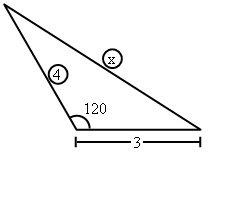Resolución:

Trazamos una altura asi como se idica en la figura

Ahora aplicaremos el teorema de euclides el segunod caso, ya que s etrata de un triangulo obtusangulo

x2 = 42 + 32 +2(3)(2); entonces calcularemos el valor de "x"

II.- TEOREMA DE LA MEDIANA

Ejemplo aplicativo:

Hallar: “x”

Aplicando el teorema de euclides

2x2 + b2/2 = 42 + 52, desarrollando esta ecuación calcularemos el valor de "x".

COMENTARIO: Los ejercicios del libro de trabajo son identicos, trata de resolverlos